What We Do
Our current research focuses on leveraging the power of artificial intelligence, especially deep learning techniques, to advance biology, medicine and healthcare. Lab members have also studied computer vision, image processing, speech processing, coding, and various machine learning techniques in the past. If you are interested in joining the group, please click here.
The group is led by Brendan J. Frey (fellow of AAAS, IEEE and RSC, and senior fellow of CIFAR) in the Department of Electrical and Computer Engineering, with cross appointments in Computer Science, Donnelly Centre for Cellular and Biomolecular Research and Vector Institute for Artificial Intelligence. Scientific inquiries and management questions are also handled by senior research scientist and lab manager Leo J. Lee.
Current Research Highlight
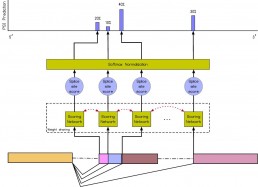
COSSMO: predicting competitive alternative splice site selection using deep learning
Our member Hannes Bretschneider presented a new splicing code at ISMB 2018 in Chicago on July 8, 2018 with a proceedings paper being simultaneously published in Oxford Bioinformatics.
The new method, COSSMO for Competitive Splice Site Model, uses deep learning to automatically learn sequence features that regulate complex splicing events with two, three, or more candidate splice sites. COSSMO can accurately predict the splice site utilization (PSI, or percent selected index) observed in RNA-seq data and we demonstrate that the features learned by COSSMO correspond to known biology such as splice site consensus motifs and splicing factor binding sites.
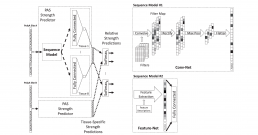
Inference of the Human Polyadenylation Code
Polyadenylation is a pervasive mechanism responsible for regulating mRNA function, stability, localization, and translation efficiency. As much as 70% of human genes are subject to alternative polyadenylation. We developed a deep learning model that can predict the tissue-specific strength of a polyadenylation site in the 3’-untranslated region of the human genome given only its genomic sequence. Without application-specific training, our human polyadenylation code can: predict which polyadenylation site is more likely to be selected in genes with multiple sites, scan the 3’-untranslated region to find candidate polyadenylation sites, classify the pathogenicity of variants near annotated polyadenylation sites in ClinVar, and anticipate the effect of antisense oligonucleotide experiments to redirect polyadenylation. The code can thus be viewed as a simulator, where the genotype of an individual can be fed in as an input, and the output describes how the individual’s mutations affect the mechanisms of polyadenylation in different tissue types.